johyeongseob 님의 블로그

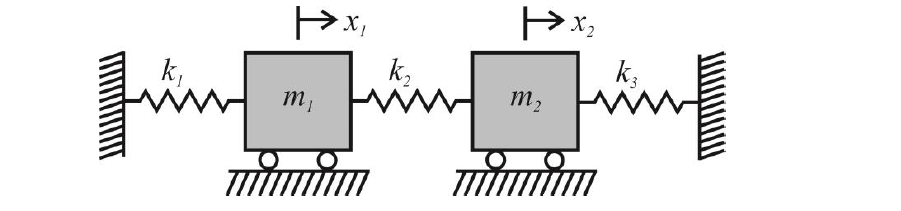
교재: Julia 프로그래밍을 활용한 구조물의 진동해석 (곽문규, 김수민) 5.1 서론  다자유진동계(Multi-Degree-of-Freedom System)는 독자적으로 움직일 수 있는 물체가 여러 개 있다는 것을 의미한다. 다자유도계의 짇농을 해석하기 위해서는 행렬의 사용이 필수적이다. 먼저 2 자유도계로 시작해보자. 5.2 비감쇠 다자유도계의 자유진동  다음과 같은 2 자유도 진동계를 고려해보자.   여기서 x₂ > x₁ 이라고 가정하고 자유물체도를 그려보자.   뉴턴 제 2법칙을 적용하여 운동방정식을 유도해보자. m₁x₁'' + (k₁ + k₂)*x₁ -k₂x₂ = 0m₂x₂'' - k₂x₁+ (k₂ + k₃)*x₂ = 0  이를 행렬식으로 간단히 표현하면 다음과 같이 쓸 수 있다. Mx'' + ..

교재: Julia 프로그래밍을 활용한 구조물의 진동해석 (곽문규, 김수민) 3.1 서론  진동학에서 가장 먼저 다루는 대상은 일자유도 진동계(Single-Degree-of-Freedom Vibration System)이다. 일반적으로 제일 단순한 스프링-질량-댐퍼로 이루어진 일자유도 진동계를 가지고 기초적인 진동이론을 설명한다. 스프링은 강성이 있으나 질량이 없는 요소이다. 그리고 강성은 Hooke의 법칙을 따른다고 가정한다. 질량은 질량만 있는 블록이며 강성은 없는 요소이다. 댐퍼는 질량은 없고 속도에 저항하는 요소이다. 각 요소를 수학식으로 표현하면 다음과 같다. Hooke law: $Fs = ks$,    Newton 2nd law: $Fm = mx''$,    Viscous Damper: $Fd ..

교재: Julia 프로그래밍을 활용한 구조물의 진동해석 (곽문규, 김수민) 2.1 미분방정식  공학과 미분방정식은 어떻게 연결되어 있을까? 미분은 변화율을 나타낸다. 즉, 미분방정식은 변화를 설명하는 식이라고 말할 수 있다. 그리고 공학 문제 대부분은 이 변화를 예측하는 것과 관련이 있다. 공과대학에서 공부하는 역학 과목들은 대부분 뉴턴 역학에 기반을 두고 있다. 역학 문제들은 공간상의 변화 또는 시간상의 변화에 관한 식으로 귀결된다. 즉, 미분방정식을 얻게 된다.  먼저 종속변수가 하나인 상미분방정식(ODE, Ordinart Differential Equation)을 살펴보자. ODE는 오른쪽 항이 0이면 제차(homogeneous)이고 종속변수의 함수이면 비제차(non-honogeneous)로 나뉜다..

교재: Julia 프로그래밍을 활용한 구조물의 진동해석 (곽문규, 김수민) 1.1 진동 이론을 왜 공부하는가?  진동은 구조물이 반복적으로 움직이는 현상을 말한다. 진동을 일으키기 위해서는 진동을 유발하는 기진력(excitation force)이 있어야 한다. 그런데 진동을 심각하게 만드는 한가지 원인이 더 존재한다. 공진(resonance)이라는 현상으로 기진력의 어떤 특정 진동수에 의해 구조물이 매우 심하게 진동하는 현상을 기리킨다. 이 진동수를 고유진동수(Natural Frequency)라고 말한다. 이는 구조물의 종류와 형태에 따라 모두 다르게 나타난다. 그래서 구조물을 설계할 때 그 구조물의 고유진동수를 구하는 것이 필요하다.  진동이라는 현상은 구조물의 움직임이 반복된다는 것을 나타내기에 시간..