논문: https://arxiv.org/abs/2106.09685
저자: Edward Hu* Yelong Shen* Phillip Wallis Zeyuan Allen-Zhu Yuanzhi Li SheanWang Lu Wang Weizhu Chen (Microsoft Corporation)
*Equal contribution
인용: Hu, Edward J., et al. "Lora: Low-rank adaptation of large language models." arXiv preprint arXiv:2106.09685 (2021).
깃허브: https://github.com/microsoft/LoRA
0. 초록 (Abstract)
NLP에 대한 주요 인식은 일반적인 데이터로 대규모 사전학습한 모델을 특정 task나 용도에 맞게 적용 (Adaptation)하는 작업이다. 우리가 더 큰 모델을 사전학습 할수록 이를 사용하기 위해 (Full fine-tuning) 모든 파라미터를 재학습하는 작업은 비싸고 힘들어진다. 그래서 저자는 Low-Rank Adaptation 즉, LoRA를 제안한다. 이는 기존 모델의 가중치를 변경하지 않고, 모델의 layer에 학습가능한 파라미터를 추가한다. 학습하는 파라미터는 rank를 분해한 매트릭스이며, 이는 downstream task를 위한 학습 파라미터 수를 줄여준다.

1. 서론 (Introduction)
초록에서 언급했듯이, NLP 사용의 대부분은 대규모 데이터에 모델을 사전 훈련한 뒤, 다양한 downstream task에 맞게 적용한다. 해당 작업은 주로 사전 훈련한 모델의 모든 파라미터를 업데이트하는 이른바 fine-tuning이라 불린다. fine-tuning의 단점을 해결하기 위해 적은 수의 파라미터 혹은 외부 모듈을 추가하는 방법이 존재한다. 하지만 이는 모델의 depth를 늘리거나, 모델의 사용가능한 sequence length를 줄여 추론 지연 (결과 도출 시간이 길어짐)이 발생한다. 더 큰 단점은 이런 방법들이 비용측면에서는 효율적이나 성능이 기존보다 낮다. 즉, efficiency와 quality의 trade-off 가 발생한다.
저자는 위 문제를 해결할 실마리를 Li et al. (2018a); Aghajanyan et al. (2020)에서 얻었다. 해당 가설은 다음과 같다. "학습된 과적합모델 (GPT, BERT)은 사실 내재적으로 저차원 구조에 존재한다." "the learned over-parametrized models in fact reside on a low intrinsic dimension." 의역하면, "모델이 학습한 지식의 핵심은 저차원 구조를 사용한다."이며, 이는 해당 파라미터만으로 fine-tuning 이 가능하다. (Figure 1)
다음은 논문의 contribution이다.
- 사전 훈련한 모델에 작은 LoRA모듈을 추가함으로서 다양한 task에 적용할 수 있다.
- LoRA는 훈련 비용을 낮춘다.
- 간단한 linear 구조는 추론 지연 없이 도입 가능하다.
- 기존 다른 방법들과 독립적이라 (orthogonal) 병행 사용이 가능하다.
2. 문제 정의 (Problem Statement)
oRA는 다양한 분야에 쓰일 수 있으며, 현재 목적에 맞게 conditional language modeling에 초점을 둔다. 사전 훈련된 augoregressive 언어모델 (ex. GPT)을 $P_\Phi(y|x)$라 하자. $\Phi$는 모델의 파라미터이다. downstream task가 요약이라 가정하면, $x$는 신문 내용, $y$는 요약문이다. full fine-tuning에서 목적함수는 다음과 같다.
\begin{align*}
& \max_\Phi \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log (P_\Phi(y_t \mid x, y_{<t}))
,
\tag{1}
\end{align*}
$\Phi_0$은 사전 학습된(pre-trained) 모델의 파라미터이다. $\Phi$는 다운스트림 작업(task)에 대해 학습된 모델의 파라미터이다. $\Delta \Phi$ 는 $\Phi$ - $\Phi_0$이다. 즉 파라미터 변화량이다. LoRA에서 목적함수는 다음과 같다.
\begin{align*}
& \max_\Theta \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log (P_{\Phi_0+\Delta\Phi(\Theta)}(y_t \mid x, y_{<t}))
,
\tag{2}
\end{align*}
반면 LoRA는 $\Delta \Phi$ = $\Delta \Phi(\Theta)$이다. $|\Theta| \ll |\Phi_0|$ 이다. GPT-3(175B) 기준 $|\Theta|$는 $|\Phi_0|$의 0.01%이다.
3. AREN’T EXISTING SOLUTIONS GOOD ENOUGH?
(생략)
4. 제안 방법 (Our Method)
LoRA의 구조와 장점에 대해 살펴보자. LoRA는 어느 dense layer(MLP)에도 사용가능하나, 여기서는 Transformer language models에 적용해보자.
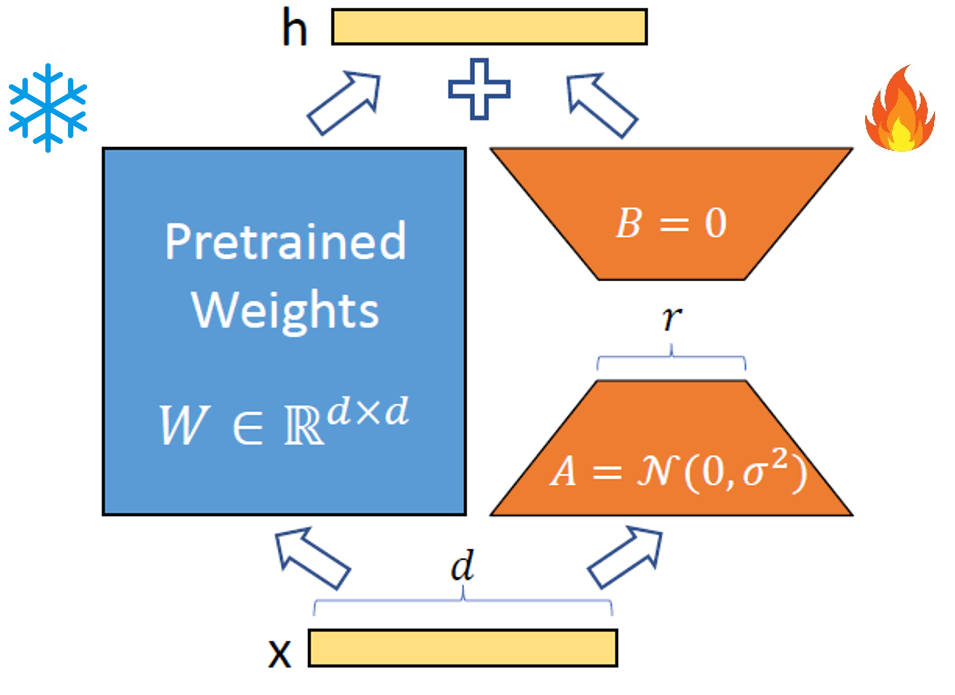
4.1 Low-Rank-Parameterized Updatae Matrices
Aghajanyan et al. (2020)에서 영감을 받아, 저자는 모델이 downstream task 적용에서 가중치 (파라미터) 업데이트가 저랭크 차원에서 이루어진다고 가정한다. $h = W_0x$라 정의하면 학습 방식은 아래와 같다.
\begin{align*}
& h = W_0x + \Delta Wx = W_0x + BAx
,
\tag{2}
\end{align*}
$W_0 \in \mathbb{R}^{d \times k} $에서 업데이트 되는 부분은 $\Delta W$이며 이는 $BA$로 표현할 수 있다. $B=\mathbb{R}^ {d \times r}, A = \mathbb{R}^ {r \times k}$ 이며 $r \ll min(d,k)$이다. 훈련 시작점에서 $A$는 random gaussian initialization이며 $B$는 0이다.
5. 실험 결과 (Empirical Experiments)
실험 조건은 다음과 같다.
- Model: RoBERTa, DeBERTa, GPT-2, GPT-3 175B
- Benchmark: General Language Understanding Evaluation (GLUE), E2E NLG (Natural Language Generation) Challenge, WikiSQL, MNLI-m, SAMSum
실험 결과는 다음과 같다. 모든 결과지표는 높은수록 좋다.
5.2 RoBERTa base/large
5.3 DeBERTa XXL

5.4 GPT-2 medium/large

5.5 Scaling up to GPT-3 175B


6. Related Works
(생략)
7. Conclusion and Future Work
거대 언어 모델의 fine-tuning 작업은 하드웨어 관점에서 비싸다. 이에 LoRA는 성능을 유지하며, 추론 지연이나 입력 문장 길이 제한 없이 fine-tuning에 성공하였다. 더욱 중요한 점은 사전 훈련한 모델의 파라미터를 유지하며, 다양한 작업에 쉽게 적용될 수 있다.
8. LoRA Pytorch 코드
해당 코드는 Convolution layer에 LoRA가 적용되는 코드이며, Microsoft github에서 제공하는 코드 중 일부입니다.
class Embedding(nn.Embedding, LoRALayer):
# LoRA implemented in a dense layer
def __init__(
self,
num_embeddings: int,
embedding_dim: int,
r: int = 0,
lora_alpha: int = 1,
merge_weights: bool = True,
**kwargs
):
nn.Embedding.__init__(self, num_embeddings, embedding_dim, **kwargs)
LoRALayer.__init__(self, r=r, lora_alpha=lora_alpha, lora_dropout=0,
merge_weights=merge_weights)
# Actual trainable parameters
if r > 0:
self.lora_A = nn.Parameter(self.weight.new_zeros((r, num_embeddings)))
self.lora_B = nn.Parameter(self.weight.new_zeros((embedding_dim, r)))
self.scaling = self.lora_alpha / self.r
# Freezing the pre-trained weight matrix
self.weight.requires_grad = False
self.reset_parameters()
def reset_parameters(self):
nn.Embedding.reset_parameters(self)
if hasattr(self, 'lora_A'):
# initialize A the same way as the default for nn.Linear and B to zero
nn.init.zeros_(self.lora_A)
nn.init.normal_(self.lora_B)
def train(self, mode: bool = True):
nn.Embedding.train(self, mode)
if mode:
if self.merge_weights and self.merged:
# Make sure that the weights are not merged
if self.r > 0:
self.weight.data -= (self.lora_B @ self.lora_A).transpose(0, 1) * self.scaling
self.merged = False
else:
if self.merge_weights and not self.merged:
# Merge the weights and mark it
if self.r > 0:
self.weight.data += (self.lora_B @ self.lora_A).transpose(0, 1) * self.scaling
self.merged = True
def forward(self, x: torch.Tensor):
if self.r > 0 and not self.merged:
result = nn.Embedding.forward(self, x)
after_A = F.embedding(
x, self.lora_A.transpose(0, 1), self.padding_idx, self.max_norm,
self.norm_type, self.scale_grad_by_freq, self.sparse
)
result += (after_A @ self.lora_B.transpose(0, 1)) * self.scaling
return result
else:
return nn.Embedding.forward(self, x)
위 코드 중, reset_parameters(self) 함수에서 A와 B를 각각 random gaussian과 0으로 초기화함을 알 수 있다. 또한 forward(self, x: torch.Tensor) 함수에서 $\Delta Wx=BAx$ 를 확인할 수 있다.
'[논문 리뷰] > 자연어처리' 카테고리의 다른 글
| [논문 리뷰] Visual Instruct Tuning (LLaVA) (0) | 2025.01.15 |
|---|---|
| [논문 리뷰] DoRA: Weight-Decomposed Low-Rank Adaptation (0) | 2024.12.27 |
| [논문 리뷰] Seq2Seq: Sequence to Sequence Learning with Neural Networks (0) | 2024.12.10 |
| [논문 리뷰] LSTM: Long Short-Term Memory (0) | 2024.12.03 |
| [논문 리뷰] Attention: Neural Machine Translation by Jointly Learning to Align and Translate (0) | 2024.11.29 |