교재: Julia 프로그래밍을 활용한 구조물의 진동해석 (곽문규, 김수민)
3.1 서론
진동학에서 가장 먼저 다루는 대상은 일자유도 진동계(Single-Degree-of-Freedom Vibration System)이다. 일반적으로 제일 단순한 스프링-질량-댐퍼로 이루어진 일자유도 진동계를 가지고 기초적인 진동이론을 설명한다. 스프링은 강성이 있으나 질량이 없는 요소이다. 그리고 강성은 Hooke의 법칙을 따른다고 가정한다. 질량은 질량만 있는 블록이며 강성은 없는 요소이다. 댐퍼는 질량은 없고 속도에 저항하는 요소이다. 각 요소를 수학식으로 표현하면 다음과 같다.
Hooke law: $Fs = ks$, Newton 2nd law: $Fm = mx''$, Viscous Damper: $Fd =cx'$
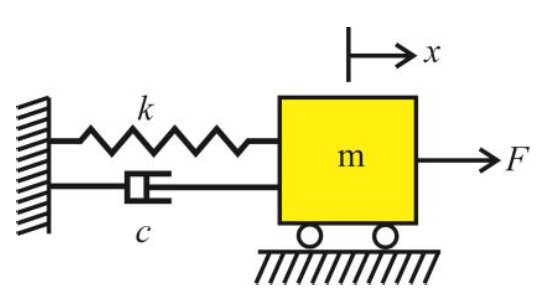

그림1에서 x는 질량의 질량 m의 변위를 나타내고 F는 이 질량에 작용하는 외력을 나타낸다. 그림2는 자유물체도이다. 자유물체도에 뉴턴 제 2법칙을 적용하면 다음과 같이 쓸 수 있다.
$\sum F_x=-ks-cx'+F=mx''$
이 식으로부터 다음과 같은 운동방정식이 유도된다. 이는 일자우도 진동계의 움직임을 표현하는 가장 기본적인 미분방정식이다.
$mx'' + cx' + kx = F$
3.2 비감쇠 자유 진동
진동학에서 가장 기본적인 비감쇠 자유진동을 고려해 보자. 비감쇠라는 것은 c = 0, 자유진동은 외부기진력인 F(t) = 0 이라는 것을 의미한다.
$mx'' + kx = 0$
즉, 질량과 스프링만 있는 진동계인 것인데 이를 풀기 위해서는 초기조건, $x(0) = x_0, \quad x'(0) = v_0$가 필요하다. 우리는 기호를 그대로 사용해 일종의 공식을 유도하여 일반화하고자 한다.
$x'' + \frac{k}{m}\times x = 0$
여기서 다음과 같은 파라미터를 하나 도입해보자.
$\omega_n = \sqrt{\frac{k}{m}}$
그러면 다음과 같이 표현된다.
$x''+(\omega_n)^2 \times x=0$
위 식을 지수법 $x(t) = A \times e^{st}$ 을 이용하여 풀면 특성방정식의 해은 $s = \pm i \omega$ 이다. 그러므로 일반해를 오일러 공식을 사용해 표현하면 $x = A \cos (\omega t) + B \sin (\omega t)$로 표현할 수 있다. 여기에 초기조건을 적용하면 해는 다음과 같이 표현된다.
$x=x_0\times \cos (\omega_n t)+\frac{V_0}{\omega_n}\times \sin (\omega_n t)$
위 식을 살펴보면 시간이 지나가면서 x가 왕복운동하는 것을 알 수 있다. 왕복하는 주기를 결정하는 파라미터가 $\omega_n$인데 이를 진동계의 고유진동수라고 부른다. 단위는 rad/s이다. 진동해석에서는 Hz(cycle/s)단위를 주로 사용한다.
$f_n=\frac{\omega_n}{2\pi}$ (Hz)
고유진동수가 중요한 이유는 초기조건에 상관없이 왕복하는 진동수는 변하지 않기 때문이다. 질량과 스프링 상수만 결정되면 진동계의 거동은 일정한 고유진동수로 자유진동을 한다는 의미이다.
스프링-질량계가 수직운동을 하게 되면 어떻게 될까?


뉴턴 제2법칙을 적용하면 다음과 같다.
$ \sum F_x=mg-kx=mx''$
그래서 운동방정식은 다음과 같다.
$mx'' + kx = mg$
우항이 상수이므로 일반해는 다음과 같이 표현된다.
$x(t) = y(t) +c$
이를 EOM에 대입하면 $my'' + ky + kc = mg$로 나타나는데 여기서 $c=\frac{mg}{k}=\delta _{st}$ 를 만족한다면, 식은 다음과 같이 변환된다.
$my'' + ky = 0$
이는 수평운동 미분방정식과 형태가 동일하다는 것을 알 수 있다. 그리고 우리가 도입한 $\delta _{st}$ 는 정적변형, 즉 m에 의한 처짐이라는 것을 알 수 있다. 정적 처짐이 발생하는 구조물의 경우 진동은 그 정적 처짐인 $\delta _{st}$ 를 기준선으로 진동이 발생한다는 것인데, 그래서 진동해석에서 대부분의 경우 중력을 무시하고 해석을 진행한다.
이번에는 단진자를 고려해보자. 단진자의 경우 중력에 의한 왕복 운동이 발생하기 때문에 중력을 무시하면 안 된다.
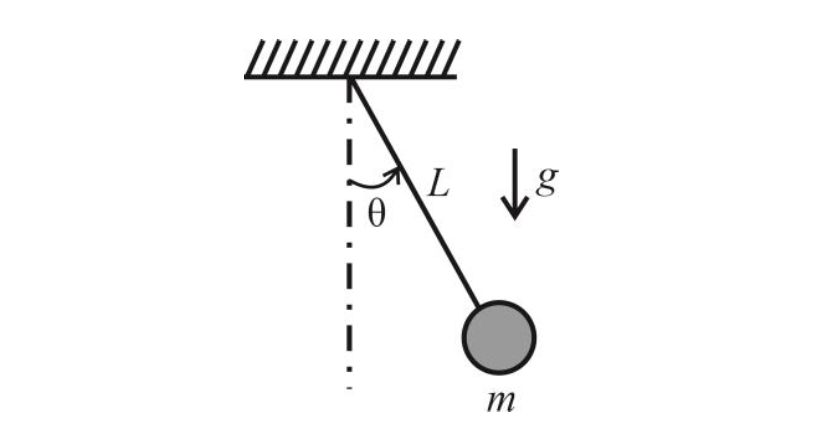

뉴턴 제2법칙을 적용하면 다음과 같다.
$\sum F_x=-T+mg\times \cos \theta =m\times a_r,\quad \sum f_\theta =-mg\times \sin \theta =m\times a\theta$
극좌표계에서 가속도 성분은 다음과 같다.
$a_r=r''-r(\theta ')^2,\quad a\theta =r\theta ''+2(r')\times (\theta ')$
줄의 길이는 변하지 않기 때문에
$r = L, \quad r' = r'' = 0$
다시 가속도 성분을 다음과 같이 쓸 수 있다.
$a_r=-L(\theta ')^2, \quad a\theta =L\theta '' $
단진자의 왕복 운동에 대한 미분방정식(운동방정식)은 다음과 같다. (if θ small, sinθ ≈ θ)
$\theta ''+(\frac{g}{L})\times \theta =0$
추가로 ωₙ = (g/L)^0.5라고 하면 다음과 같다.
$\theta ''+(\omega _n^2)\times \theta =0$
이는 비감쇠 자유진동과 비슷함을 알 수 있다.
3.3 에너지 방법
위에서 뉴턴 제 2법칙을 살펴보았다. 이번에 살펴볼 에너지 방법은 운동에너지와 위치에너지, 즉 스칼라양을 이용하기 때문에 뉴턴 제 2법칙에 비해 간단하다고 말할 수 있다. 위 비감쇠 자유진동을 다시 살펴보자.

이 경우 운동에너지(Kinetic, T)와 위치에너지(Potential-spring, V)는 다음과 같이 표현된다.
$T=\frac{1}{2}m(x')^2,\quad V=\frac{1}{2}k(x^2) $
에너지 보존법칙이 T + V = constant이므로 시간에 대한 미분값이 0이 나온다.
$\frac{d}{dt}[\frac{1}{2}m(x')^2+\frac{1}{2}k(x^2)]$
이를 정리하면 다음과 같이 나온다.
$mx'' + kx = 0$
단진자 운동에 대해서도 운동에너지와 위치에너지는 다음과 같다.
$T=\frac{1}{2}m(L\theta ')^2, \quad V=mgL(1-\cos \theta )$
이를 같은 방법으로 적용하면 운동방정식이 다음과 같이 유도된다.
$mL^2\theta ''+mgL \sin \theta =0$
3.4 감쇠 자유 진동
앞 절의 모델에 댐퍼를 추가해 보자.

이 경우에 대한 운동방정식은 다음과 같다.
$mx'' + cx' + kx = 0$
감쇠(Damper)는 에너지를 소산하는 역할을 담당한다. 특히 선형 형태로 나타나는 이런 감쇠를 점성 감쇠(Viscous damper)라고 부른다. 다음과 같은 파라미터들을 도입해 보자.
$\frac{c}{m}=2\zeta \omega _n, \quad \frac{k}{m}=(\omega_n)^2$
여기서 ξ는 감쇠인자(damping factor)라고 부른다. 운동방정식을 다음 파라미터로 표현될 수 있다.
$x''+2\zeta \omega _nx'+(\omega _n)^2x=0$
특성방정식과 해는 다음과 같다.
$s^2+2\zeta \omega _ns+(\omega _n)^2=0,\quad s=[-\zeta \pm \sqrt{\zeta^2-1}]\times \omega_n$
해를 살펴보면 3가지 경우가 나올 수 있다.
- 0 < ξ < 1(부족감쇠, underdamped): $s=-\zeta \omega _n\pm i\omega d,\quad \omega d=[\sqrt{1-\zeta^2}]\times \omega _n $, ωd: 감쇠 고유진동수
- ξ = 1(임계감쇠, critically): s1 = s2 = -ωₙ
- ξ > 1(과감쇠, overdamped): $s=[-\zeta \pm \sqrt{\zeta^2-1}]\times \omega_n$
1. 부족감쇠에서 감쇠가 작은 경우 $\omega_d$와 ωₙ은 거의 같다. 그런 경우 감쇠 고유진동수와 고유진동수를 구분하지 않는다. 부족감쇠의 경우 미분방정식의 해는 다음과 같이 표현된다.
$x=A\times e^{(-\zeta \omega_nt)}\times \cos (\omega_d \times t-\phi)$
여기서 $\phi$는 위상차, 즉 시간 지연을 나타낸다. A는 진폭(Amplitude)이라고 부른다. 비감쇠 자유진동이며 부족 감쇠의 경우 두 가지 특징이 있다. $\omega_d$의 진동수로 진동하는 항과 -ξωₙt로 감소하는 지수항이 곱해져 있다. 그래서 진폭이 지수적으로 감소하면서 진동한다고 예상할 수 있다.
예제) $m = 1kg,\quad c = 2Ns/m,\quad k = 10N/m$, 초기조건: $x(0) = x_0 = 1m,\quad x'(0) = v_0 = 0m/s$
using Plots
m = 1; c=2; k=10; x0 = 1; v0=0;
ωn = sqrt(k/m);
ζ = c/(2*m*ωn);
ωd = sqrt(1-ζ^2)*ωn;
A=sqrt(x0^2+((v0+ζ*ωn*x0)/ωd)^2)
ph = atan(v0+ζ*ωn*x0,ωd*x0);
t=0:0.01:10
x = A*exp.(-ζ*ωn*t).*cos.(ωd*t.-ph);
p=plot(t,x,label="x(t)")
display(p)

2. 임계감쇠에서 해는 다음과 같이 나온다.
$x=A_1\times e^{-\omega_nt}+A_2\times t\times e^{-\omega_nt}$
초기조건 $x(0) = x_0,\quad x'(0) = v_0$을 적용하면
$x=[x_0+(v_0+\omega _n\times x_0)\times t]\times e^{-\omega_nt}$
식을 살펴보면 시간에 비례해서 변화하는 항과 시간이 지남에 따라 지수적으로 감소하는 항이 곱해져 있는 것을 알 수 있다. 지수적으로 감소하는 항이 더 빨리 0으로 수렴하기 때문에 x(t)는 0으로 수렴하게 된다. 삼각함수 항이 없기에 진동은 하지 않는다.
3. 과감쇠인 경우 $\sqrt{\zeta^2-1}<\zeta$ 이므로 진동이 일어나지 않기에 더 이상 자세하게 소개하지 않는다.
$x=A_1\times e^{[-\zeta +\sqrt{\zeta ^2 -1}]\times \omega _n\times t}+A_2\times t\times e^{[-\zeta -\sqrt{\zeta ^2 -1}]\times \omega_n\times t}$
감쇠는 진동을 억제하고자 하는 엔지니어들에게 고마운 존재이다. 감쇠 자유진동 결과에서 보여주듯이 감쇠는 시간이 흐를수록 진동의 진폭을 감소하게 한다. ζ를 구하는 방법으로는 대수 감소율을 사용한다. 이는 다음과 같다.
$\zeta \approx \frac{\delta}{2\pi}, \quad \delta =ln{\frac{x_1}{x_2}}$ $x_1, x_2$ = 첫 번째 진폭과 두 번째 진폭, (ζ << 1)
3.5 조화기진력에 의한 비감쇠 진동계의 강제진동
감쇠가 없고 조화기진력(F)이 작용하는 경우를 고려해보자.

위 그림의 진동계에 대한 운동방정식은 다음과 같다.
$mx'' + kx = F$
그리고 초기조건이 모두 0이라고 하고 $F = F_0\times \sin (\omega t)$로 조화기진력이 작용하고 있다고 하자. $F_0 = kf_0$라고 하면 식을 다음과 같이 표현할 수 있다. 여기서 ω는 조화기진력의 진동수이다.
$x''+\omega_n^2\times x=\omega _n^2\times f_0\times \sin (\omega t) $
진동문제에서 외부기진력이 가해지는 경우에는 미분방정식의 특수해(Particular solution)만 관심이 있다. homogeneous는 시간이 지나면 사라지기 때문이다. 특수해는 $x_p=A\times \sin(\omega t)+B\cos(\omega t)$이다. 특수해를 시간에 대해 미분하면 속도와 가속도를 구할 수 있다. 이를 미분방정식에 대입하면 다음과 같다.
$A(\omega _n-\omega ^2)\times \sin (\omega t)+B(\omega _n^2-\omega ^2)\times \cos (\omega t)=\omega _n^2\times f_0\times \sin (\omega t)$
sin(ωt) 와 cos(ωt)는 시간에 대한 변함이기에 0이 되면 안 된다. 그러므로 계수들이 0이 되면 미지수 A, B를 구할 수 있다. 또한 기진력 진동수와 고유진동수의 비를 r로 정의하면, 우리는 특수해를 다음과 같이 표현할 수 있다.
$x_p=(\frac{f_0}{1-r^2})\times \sin (\omega t), \quad r=\frac{\omega}{\omega_n}$
이로부터 조화기진력과 유사한 기진원이 있는 경우 기진력의 진동수보다 낮은 고유진동수를 갖는 구조물을 설계하면 구조물의 진동을 작게 만들 수 있음을 예상할 수 있다. 또한 구조물을 설계할 때 ω = ωₙ, 즉 공진은 위험한 결과를 초래함을 위 식이 알려준다.
3.6 조화기진력에 의한 감쇠 진동계의 강제진동
감쇠가 추가된 진동계에 조화기진력 F가 작용하는 경우를 고려해보자.

댐퍼가 추가된 진동계에 대한 운동방정식은 $cx'$을 추가한 $mx'' + cx' + kx = F_0\times \sin (\omega t)$이며 $F_0\times kf_0$을 도입하여 다시 쓰면 다음과 같다.
$x''+2\zeta \omega _n\times x'+\omega_n^2\times x=\omega _n^2\times f_0\times \sin (\omega t)$
마찬가지로 초기조건을 모두 0, 특수해가 $x=A\times \sin (\omega t)+B\times \cos (\omega t)$일 경우 시간에 대한 미분으로 속도와 가속도를 구해 위 식에 대입하면 다음과 같은 결과가 나온다.
$(-\omega ^2\times A-2\zeta \omega _n\times \omega \times B+\omega _n^2\times A)\sin (\omega t)+(-\omega ^2\times B+2\zeta \omega _n\times \omega \times A+\omega _n^2\times B)\cos (\omega t)=\omega _n^2\times f_0\times \sin (\omega t)$
무차원 변수 $r=\frac{\omega}{\omega_n}$을 도입하여 A, B를 구한 후, 이를 $x_p$에 대입하면 다음과 같이 정리할 수 있다.
$x=(\frac{f_0}{(1-r^2)^2+(2\zeta r)^2}) \times [(1-r^2)\sin (\omega t)-(2\zeta r)\cos (\omega t)]$
이 식은 아래 유도과정에 따라 다음과 같이 다시 표현할 수 있다.
$x=f_0\times G\times \sin (\omega t-\phi), \quad G=\frac{1}{\sqrt{(1-r^2)^2+(2\zeta r)^2}}, \quad \phi = \tan^{-1}[\frac{2\zeta r}{1-r^2}]$
여기서 G는 증폭 크기(Magnitude), $\phi$는 위상차(phase)라고 불린다.

G, Φ는 여러 ζ값에 대해서 다음 그림과 같다.( 파란색(ζ=0.01) < 주황색 < 초록색 < 보라색 < 갈색(ζ=1) )
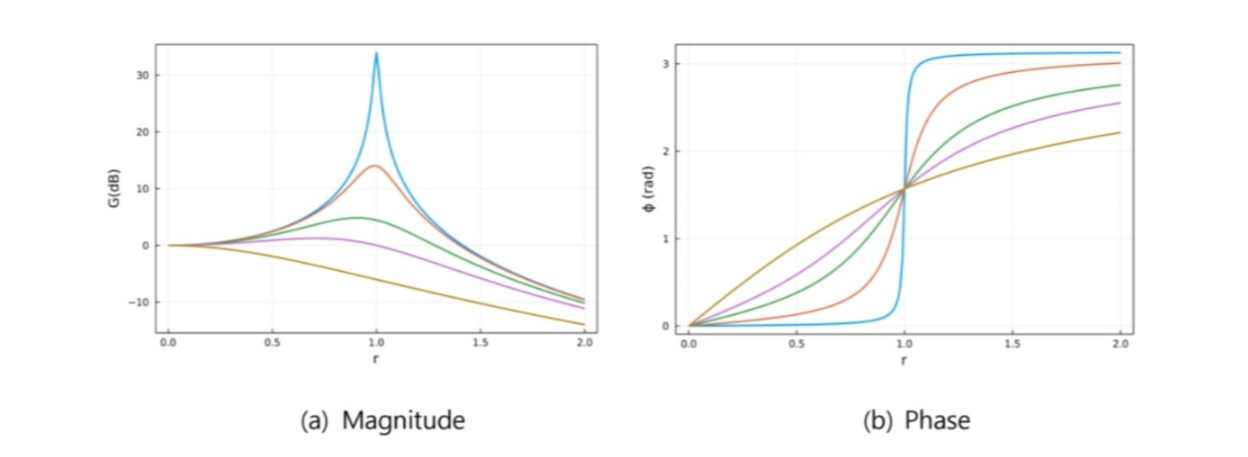
위 그림으로부터 ζ가 작을수록 공진(r = 1)시의 피크가 커지는 것을 볼 수 있다. 반대로 댐핑이 큰 경우 공진에도 진폭이 작아짐을 알 수 있다. 공진이 아닌 경우(양 끝)에는 damping과 관련이 없다는 것을 알 수 있다.
'기계공학 > 진동및소음' 카테고리의 다른 글
| [기계공학/진동및소음] 05. 다자유도의 진동해석 (0) | 2024.09.19 |
|---|---|
| [기계공학/진동및소음] 02. 기본 수학1 (0) | 2024.09.18 |
| [기계공학/진동및소음] 01. Introduction (0) | 2024.09.18 |