8.1 트리의 개념
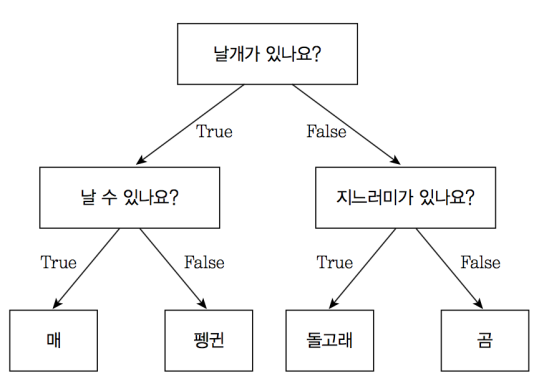
만약 자료가 계층적인 구조(hierarchical structure)를 가지고 있다면 리스트, 스택, 큐 등의 선형 자료 구조(linear data structure)는 더 이상 적합하지 않다. 트리(tree)는 이러한 계층적인 자료를 표현하는데 적합한 자료구조이다. 트리는 인공 지능 문제에서도 사용된다. 대표적인 것이 결정 트리(decision tree)이다. 결정 트리는 인간의 의사 결정 구조를 표현하는 한 가지 방법이다. 이러한 구조를 트리라고 부르는 이유는 마치 실제 트리를 거꾸로 엎어놓은 것 같은 모양을 하고 있기 때문이다.
트리의 용어들
트리의 구성 요소를 노드(node)라 한다. 트리는 한 개 이상의 노드로 이루어진 유한 집합이다. 이들 중 하나의 노드는 루트(root) 노드라 불리고 나머지 노드들은 서브 트리(subtree)라고 불린다. 계층적인 구조에서 가장 높은 곳에 있는 노드가 루트이다. 트리에서 루트와 서브트리는 선으로 연결된다. 이 연결선을 간선(edge)라고 한다. 노드들 간에는 부모 관계, 형제 관계, 조상과 자손 관계가 존재한다. 조상 노드(ancestor node)란 루트 노드에서 임의의 노드까지의 경로를 이루고 있는 노드들을 말한다. 후손 노드(descendent node)는 임의의 노드 하위에 연결된 모든 노드들을 의미한다. 자식 노드가 없는 노드를 단말노드(terminal node, 또는 leaf node)라고 한다. 그 반대가 비단말 노드(nonterminal node)이다. 노드의 차수(degree)는 어떤 노드가 가지고 있는 자식 노드의 개수를 의미한다. 트리에서 레벨(level)은 트리의 각층에 번호를 매기는 것으로서 루트의 레벨은 1이 되고 한 층씩 내려갈수록 1씩 증가한다. 트리의 높이(height)는 트리가 가지고 있는 최대 레벨을 말한다. 마지막으로 트리들의 집합을 포리스트(forest)라고 한다.
8.2 이진 트리 소개
이진 트리의 정의
트리 중에서 가장 많이 쓰이는 트리가 이진트리이다. 모든 노드가 2개의 서브 트리를 가지고 있는 트리를 이진 트리(binary tree)라고 한다. 이진 트리의 정의는 다음과 같다.
- 공집합이거나
- 루트와 왼쪽 서브 트리, 오른쪽 서브 트리로 구성된 노드들의 유한 집합으로 정의된다. 이진트리의 서브트리들은 모두 이진트리여야 한다.
이진트리와 일반 트리의 차이점은 다음과 같다.
- 이진트리의 모든 노드는 차수가 2 이하이다. 반면 일반 트리는 자식 노드의 개수에 제한이 없다.
- 일반 트리와는 달리 이진 트리는 노드를 하나도 갖지 않을 수도 있다.
- 서브 트리 간에 순서가 존재한다는 점도 다른 점이다. 왼쪽 서브트리와 오른쪽 서브트리를 구별한다.
이진 트리의 성질은 다음과 같다.
- n개의 노드를 가진 이진트리는 정확하게 n-1개의 간선을 가진다.
- 높이가 h인 이진트리의 경우, 최소 h개의 노드를 가지며 최대 2ᵏ-1개의 노드를 가진다.
- n개의 노드를 가지는 이진 트리의 높이는 최대 n이거나 최소 ⌈log₂(n+1)⌉이 된다.
이진트리의 분류
이진트리는 포화 이진 트리(full binary tree), 완전 이진 트리(complete binary tree), 기타 이진 트리로 분류할 수 있다. 포화 이진 트리는 각 레벨에 노드가 꽉 차있는 이진트리를 의미한다. 완전 이진 트리는 높이가 k일 때 레벨 1부터 k-1까지는 노드가 모두 채워져 있고 마지막 레벨 k에서는 왼쪽부터 오른쪽으로 노드가 순서대로 채워져 있는 이진트리이다. 마지막 레벨에서는 노드가 꽉 차있지 않아도 되지만 중간에 빈 곳이 있어서는 안 된다. 그 외에는 기타 이진 트리이다.
8.3 이진 트리의 표현
링크 표현법
링크 표현법에서는 트리에서의 노드가 구조체로 표현되고, 각 노드가 포인터를 가지고 있어서 이 포인터를 이용하여 노드와 노드를 연결하는 방법이다. 이진트리를 링크 표현법으로 표현하여 보면 하나의 노드가 3개의 필드를 가지는데, 데이터를 저장하는 필드와 왼쪽 자식노드와 오른쪽 자식노드를 가리키는 2개의 포인터 필드를 가진다. 이 2개의 포인터를 이용하여 부모노드와 자식노드를 연결한다.
구조체를 이용하여 노드의 구조를 정의하고 링크는 포인터의 개념을 이용하여 정의하면 된다. 링크법으로 표현된 트리는 루트 노드를 가리키는 포인터만 있으면 트리 안의 모든 노드들에 접근할 수 있다. 이것은 연결 리스트와 아주 유사한데, 연결 리스트도 포인터에 의하여 연결된 구조이기 때문이다. 연결 리스트는 1차원적인 연결된 구조라면 링크법으로 표현된 이진 트리는 2차원적으로 연결된 구조라 할 수 있다.
typedef struct TreeNode {
int data;
struct TreeNode* left, * right;
} TreeNode;
8.4 이진 트리의 순회
이진 트리를 순회(traversal)한다는 것은 이진 트리에 속하는 모든 노드를 한 번씩 방문하여 노드가 가지고 있는 데이터를 목적에 맞게 처리하는 것을 의미한다.
이진 트리의 순회방법
이진 트리를 순회하는 표준적인 방법에는 전위, 중위, 후위의 3가지 방법이 있다. 이는 루트의 왼쪽 서브트리, 오른쪽 서브트리 중에서 루트를 언제 방문하느냐에 따라 구분된다. 즉 루트를 서브 트리에 앞서서 먼저 방문하면 전위순회, 루트를 왼쪽과 오른쪽 서브트리 중간에 방문하면 중위순회, 루트를 서브 트리 방문 후에 방문하면 후위 순회가 된다. 여기서 항상 왼쪽 서브 트리를 오른쪽 서브 트리에 앞서서 방문한다고 가장하자. 각 서브트리도 전체 이진 트리와 같은 방법을 적용한다. 따라서 전체 순회에 사용된 알고리즘을 다시 서브 트리에 적용한다.
- 전위순회(preorder traversal): VLR
- 중위순회(inorder traversal): LVR
- 후위순회(postorder traversal): LRV
이진 트리의 3가지 순회 방법
// 전위 순회
preorder(TreeNode* root) {
if (root) {
printf("%d", root->data); // 노드 방문
preorder(root->left); // 왼쪽서브트리 순회
preorder(root->right); // 오른쪽서브트리 순회
}
}
// 중위 순회
inorder(TreeNode* root) {
if (root) {
inorder(root->left); // 왼쪽서브트리 순회
printf("%d", root->data); // 노드 방문
inorder(root->right); // 오른쪽서브트리 순회
}
}
// 후위 순회
postorder(TreeNode* root) {
if (root) {
postorder(root->left); // 왼쪽 서브 트리 순회
postorder(root->right); // 오른쪽 서브 트리 순회
printf("%d", root->data); // 노드 방문
}
}
8.11 이진 탐색 트리
이진 탐색 트리(binary search tree)는 이진 트리 기반의 탐색을 위한 자료이다. 탐색은 컴퓨터 프로그램에서도 많이 사용되며, 가장 시간이 많이 걸리는 작업 중의 하나이므로 탐색을 효율적으로 수행하는 것은 무척 중요하다.
이진 탐색 트리의 정의
- 모든 원소의 키는 유일한 키를 가진다.
- 왼쪽 서브 트리 키들은 루트 키보다 작다.
- 오른쪽 서브 트리의 키들은 루트 키보다 크다.
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.
이진 탐색 트리에서 특정한 키값을 가진 노드를 찾기 위해서는 먼저 주어진 탐색키 값과 루트 노드의 키값을 비교한다. 비교한 결과에 따라 다음의 3가지로 나누어진다.
- 비교한 결과가 같으면 탐색이 성공적으로 끝난다.
- 비교한 결과가, 주어진 키 값이 루트 노드의 키값보다 작으면 탐색은 이 루트 노드의 왼쪽 자식을 기준으로 다시 시작한다.
- 비교한 결과가, 주어진 키 값이 루트 노드의 키값보다 크면 탐색은 이 루트 노드의 오른쪽 자식을 기준으로 다시 시작한다.
다음 프로그램은 반복적인 기법으로 탐색 연산을 구현한 것이다.
TreeNode* search(TreeNode* node, int key)
{
while (node != NULL) {
if (key == node->key) return node;
else if (key < node->key)
node = node->left;
else
node = node->right;
}
return NULL; // 탐색에 실패했을 경우 NULL 반환
}
이진 탐색 트리에서 삽입연산
이진 탐색 트리에 원소를 삽입하기 위해서는 먼저 탐색을 수행하는 것이 필요하다. 이유는 이진 탐색 트리에서는 같은 키값을 갖는 노드가 없어야 하기 때문이고 또한 탐색에 실패한 위치가 바로 새로운 노드를 삽입하는 위치가 되기 때문이다. 새로운 노드는 항상 단말노드에 추가된다. 우리는 단말 노드를 발견할 때까지 루트에서 키를 검색하기 시작한다. 단말 노드가 발견되면 새로운 노드가 단말 노드의 하위 노드로 추가된다.
TreeNode* new_node(int item)
{
TreeNode* temp = (TreeNode*)malloc(sizeof(TreeNode));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
TreeNode* insert_node(TreeNode* node, int key)
{
// 트리가 공백이면 새로운 노드를 반환한다.
if (node == NULL) return new_node(key);
// 그렇지 않으면 순환적으로 트리를 내려간다.
if (key < node->key)
node->left = insert_node(node->left, key);
else if (key > node->key)
node->right = insert_node(node->right, key);
// 변경된 루트 포인터를 반환한다.
return node;
}
이진 탐색 트리에서 삭제 연산
노드를 삭제하기 위해서 먼저 노드를 탐색하여야 한다. 삭제하려고 하는 키값이 트리 안에 어디 있는지를 알면 다음의 3가지 경우를 고려하여야 한다.
1. 삭제하려는 노드가 단말 노드일 경우
단말노드만 지우면 된다. 이는 단말 노드의 부모 노드를 찾아서 부모 노드 안의 링크필드를 NULL로 만들어서 연결을 끊으면 된다. 다음으로 동적 메모리 해제시키면 된다.
2. 삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리 중 하나만 가지고 있는 경우
자기 노드를 삭제하고 서브트리는 자기 노드의 부모 노드에 붙여주면 된다.
3. 삭제하려는 노드가 두 개의 서브 트리 모두 가지고 있는 경우
삭제되는 노드와 가장 값이 비슷한 노드를 선택하여야 한다. 이는 왼쪽 서브트리에서 가장 큰 값이나 오른쪽 서브트렝서 가장 작은 값이 삭제되는 노드와 가장 가깝다는 것을 쉽게 알 수 있다. 오른쪽 서브 트리에서 제일 작은 값을 선택한다고 하자. 그러면 삭제되는 노드의 오른쪽 서브 트리에서 왼쪽 자식 링크를 타고 NULL을 만날 때까지 계속 진행하면 된다.
TreeNode* min_value_node(TreeNode* node)
{
TreeNode* current = node;
// 맨 왼쪽 단말 노드를 찾으러 내려감
while (current->left != NULL)
current = current->left;
return current;
}
TreeNode* delete_node(TreeNode* root, int key)
{
if (root == NULL) return root;
if (key < root->key)
root->left = delete_node(root->left, key);
else if (key > root->key)
root->right = delete_node(root->right, key);
else {
// 첫 번째나 두 번째 경우
if (root->left == NULL) {
TreeNode* temp = root->right;
free(root);
return temp;
}
else if (root->right == NULL) {
TreeNode* temp = root->left;
free(root);
return temp;
}
// 세 번째 경우
TreeNode* temp = min_value_node(root->right);
// 중외 순회시 후계 노드를 복사한다.
root->key = temp->key;
// 중외 순회시 후계 노드를 삭제한다.
root->right = delete_node(root->right, temp->key);
}
return root;
}'CS과목 > 자료구조' 카테고리의 다른 글
| [CS과목/자료구조] 10 그래프 1 (0) | 2024.09.18 |
|---|---|
| [CS과목/자료구조] 09 우선순위 큐 (0) | 2024.09.15 |
| [CS과목/자료구조] 07 연결 리스트 2 (0) | 2024.09.15 |
| [CS과목/자료구조] 06 연결 리스트 1 (0) | 2024.09.15 |
| [CS과목/자료구조] 05 큐 (0) | 2024.09.15 |